-
(本题满分11分)
设总体X的概率密度函数为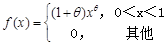 ,其中
,其中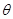 >-1为未知参数,
>-1为未知参数,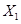 ,
,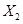 ,…,
,…,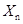 为取自总体X的容量为挖的简单随机样本.试求:
为取自总体X的容量为挖的简单随机样本.试求:
(I)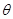 的矩估计量;
的矩估计量;
(Ⅱ)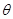 的最大似然估计量.
的最大似然估计量.
-
(本题满分11分)
设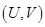 在以点
在以点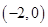 ,
,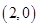 ,
,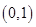 ,
,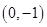 为顶点的四边形上服从均匀分布,令
为顶点的四边形上服从均匀分布,令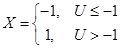 ,
,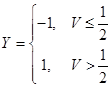 。
。
(Ⅰ)求U与V的边缘密度;
(Ⅱ)求X与Y的联合分布律;
(Ⅲ)求X与Y的协方差.
-
当x→0时,下列无穷小量中阶数最高的是( )。
-
设
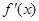 在
在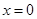 及其附近连续,
及其附近连续,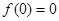 ,
,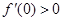 ,则下列结论正确的是( )。
,则下列结论正确的是( )。
-
设z=f(x,y)满足
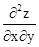 =x+y,且f(x,0)=
=x+y,且f(x,0)=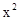 ,f(0,y)=y,则f(x,y)为( )。
,f(0,y)=y,则f(x,y)为( )。
-
设
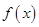 在
在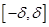 有定义,且
有定义,且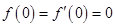 ,
,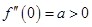 ,又
,又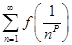 收敛,则P的取值范围是( )。
收敛,则P的取值范围是( )。
-
已知三阶矩阵A的特征值为0,
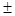 1,则下列结论中不正确的是( )。
1,则下列结论中不正确的是( )。
-
设
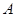 为三阶矩阵,
为三阶矩阵,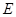 为三阶单位阵,
为三阶单位阵,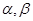 是两个线性无关的3维列向量,且
是两个线性无关的3维列向量,且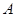 的行列式
的行列式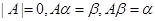 ,则行列式
,则行列式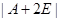 的值等于( )。
的值等于( )。
-
设
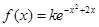 为概率密度,则
为概率密度,则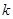 的值为( )。
的值为( )。
-
设随机变量X服从正态分布N(
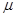 ,
,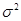 ),其分布函数为F(x),设随机变量Y=F(x),则
),其分布函数为F(x),设随机变量Y=F(x),则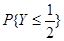 的值( )。
的值( )。
-
设
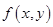 可微,
可微,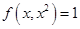 ,
,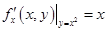 ,则
,则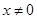 时,
时,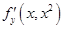 =---------。
=---------。
-
微分方程
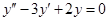 满足
满足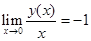 的特解为-----------。
的特解为-----------。
-
设u=
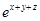 ,且y,z由方程
,且y,z由方程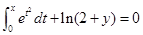 及
及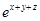 =e+1nz确定为x的函数,则
=e+1nz确定为x的函数,则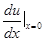 -----------。
-----------。
-
设
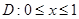 ,
,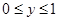 ,
,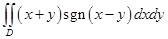 ----------。
----------。
-
已知向量组
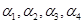 线性无关,则向量组
线性无关,则向量组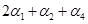 ,
,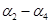 ,
,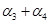 ,
,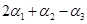 的秩为--------。
的秩为--------。
-
设随机变量
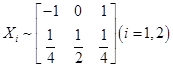 ,且满足条件
,且满足条件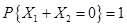 ,则
,则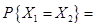 -----------。
-----------。
-
(本题满分10分)
求数列极限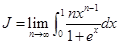 。
。
-
(本题满分10分)
设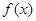 在
在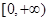 上可导且
上可导且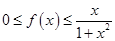 。证明:存在
。证明:存在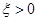 ,使
,使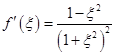 。
。
-
(本题满分10分)
设f(x)在区间[a,b]上可导,且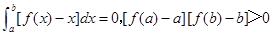 .证明存在
.证明存在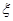 ∈(a,b),使
∈(a,b),使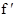 (
(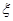 )=1.
)=1.
-
(本题满分10分)
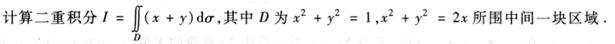
-
(本题满分10分)
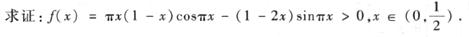
-
(本题满分11分)
已知向量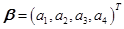 可以由
可以由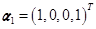 ,
,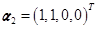 ,
,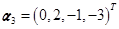 ,
,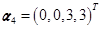 线性表出。
线性表出。
(Ⅰ)求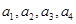 应满足的条件;
应满足的条件;
(Ⅱ)求向量组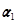 ,
,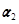 ,
,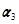 ,
,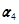 的一个极大线性无关组,并把其他向量用该极大线性无关组线性表出;
的一个极大线性无关组,并把其他向量用该极大线性无关组线性表出;
(Ⅲ)把向量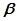 分别用
分别用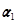 ,
,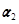 ,
,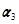 ,
,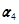 和它的极大线性无关组线性表出。
和它的极大线性无关组线性表出。
-
(本题满分11分)
已知实二次型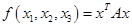 的矩阵
的矩阵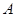 满足
满足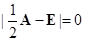 ,且
,且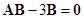 .其中
.其中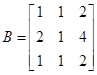 。
。
(Ⅰ)用正交变换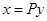 化二次型为标准型,并写出所用正交变换及所得标准型;
化二次型为标准型,并写出所用正交变换及所得标准型;
(Ⅱ)求出二次型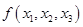 的具体表达式.
的具体表达式.
-
(本题满分11分)
设已知总体X是离散型随机变量,x的可能取值为0,1,2.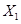 ,
,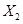 ,…,
,…,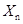 是来自总体X的简单随机样本,如果P(X=2)=(1-
是来自总体X的简单随机样本,如果P(X=2)=(1-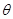 )
)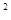 ,EX=2(1-
,EX=2(1-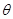 ),(0<
),(0<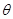 <
<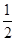 ).
).
(Ⅰ)求X的概率分布;
(Ⅱ)求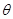 的矩估计量,并讨论其无偏性.
的矩估计量,并讨论其无偏性.
-
(本题满分11分)
设某地区在一年内发生一般性交通事故的次数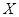 和发生重大交通事故的次数
和发生重大交通事故的次数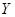 相互独立,且分别服从参数为
相互独立,且分别服从参数为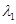 和
和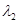 的泊松分布。试求在一年内共发生了
的泊松分布。试求在一年内共发生了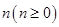 次交通事故的条件下,重大交通事故
次交通事故的条件下,重大交通事故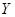 的条件概率分布。
的条件概率分布。
-
当x→∞时,函数f(x)=
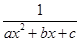 于g(x)=
于g(x)=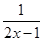 是等价无穷小,则a,b,c的取值情况为( ).
是等价无穷小,则a,b,c的取值情况为( ).
-
设函数y=f(x)是微分方程
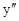 +
+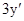 -5y=0的一个解且f(
-5y=0的一个解且f(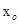 )>0,
)>0,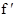 (
(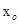 )=0,则f(x)在x=
)=0,则f(x)在x=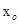 处( ).
处( ).
-
设
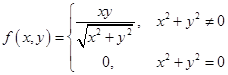 ,则在点(0,0)处,
,则在点(0,0)处,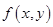 ( ).
( ).
-
设流体的流速
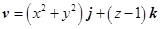 ,
,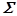 为锥面
为锥面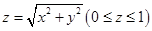 ,取下侧,则流体穿过曲面
,取下侧,则流体穿过曲面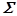 的体积流量是( ).
的体积流量是( ).
-
设
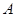 是一个
是一个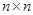 矩阵,交换
矩阵,交换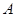 的第
的第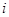 行、第
行、第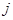 行,然后再交换其第
行,然后再交换其第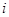 列、第
列、第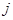 列,所得矩阵为B,考虑命题:①
列,所得矩阵为B,考虑命题:①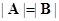 ;②
;②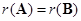 ;③A、B的行向量组等价;④A与B为相似矩阵.则以上命题成立的个数为( ).
;③A、B的行向量组等价;④A与B为相似矩阵.则以上命题成立的个数为( ).
-
设
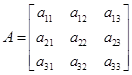 ,
,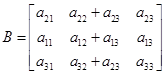 ,
,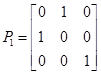 ,
,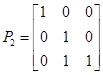 ,则必有( ).
,则必有( ).
-
设随机变量X和Y相互独立,且均服从(0,1)上的均匀分布,则下列随机变量中仍服从某区间上的均匀分布的是( ).
-
设二维离散型随机变量
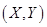 的联合概率分布如下表所示
的联合概率分布如下表所示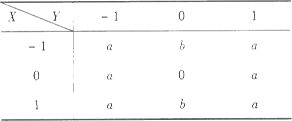 其中
其中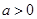 ,
,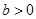 则一定有( ).
则一定有( ).
-
设
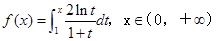 ,则f(x)+f(
,则f(x)+f(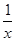 )=----------.
)=----------.
-
方程
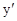 +
+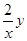 +x=0满足条件
+x=0满足条件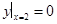 的解为----------.
的解为----------.
-
设函数
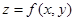 在点(0,1)的某邻域内可微,且
在点(0,1)的某邻域内可微,且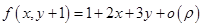 ,其中
,其中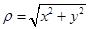 。则曲面
。则曲面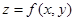 在点(0,1)处的切平面方程为----------。
在点(0,1)处的切平面方程为----------。
-
累次积分
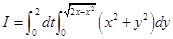 =----------。
=----------。
-
设A为三阶实对称矩阵,
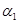 =(a,-a,1)
=(a,-a,1)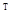 是Ax=0的解,
是Ax=0的解,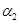 =(a,l,1-a)
=(a,l,1-a)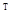 是(A+E)x=0的解,则常数a=-----------.
是(A+E)x=0的解,则常数a=-----------.
-
已知随机变量X和Y的分布律为
 而且
而且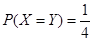 ,则X与Y的相关系数为-----------。
,则X与Y的相关系数为-----------。
-
(本题满分10分)
已知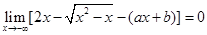 ,求a,b的值.
,求a,b的值.
-
(本题满分10分)
设可微函数f(x)满足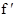 (x)+
(x)+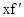 (-x)=x(-
(-x)=x(-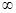 <x<+
<x<+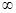 ),且f(0)=0,求f(x)的表达式.
),且f(0)=0,求f(x)的表达式.
-
(本题满分10分)
设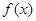 连续可导,
连续可导,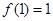 ,G为不包含原点的单连通域,任取M,N∈G,在G内曲线积分
,G为不包含原点的单连通域,任取M,N∈G,在G内曲线积分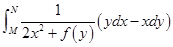 与路径无关。
与路径无关。
(Ⅰ)求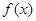 ;
;
(Ⅱ)求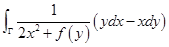 ,其中
,其中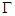 为
为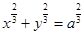 ,取正向。
,取正向。
-
(本题满分10分)
求函数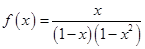 的麦克劳林展开式。
的麦克劳林展开式。
-
(本题满分10分)
计算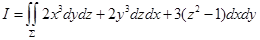 ,其中∑是曲面z=1-
,其中∑是曲面z=1-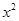 -
-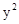 (z≥0)的上侧.
(z≥0)的上侧.
-
(本题满分11分)
设A为三阶矩阵,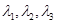 是A的三个不同的特征值,对应的特征向量为
是A的三个不同的特征值,对应的特征向量为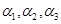 ,令
,令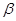 =
=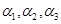 .
.
(Ⅰ)证明: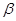 ,
,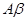 ,
,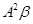 线性无关.
线性无关.
(Ⅱ)若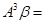
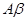 ,求秩r(A—E)及行列式|A+2E|.
,求秩r(A—E)及行列式|A+2E|.
-
(本题满分11分)
设n阶实对称矩阵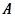 满足
满足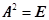 ,且秩
,且秩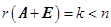 。
。
(Ⅰ)求二次型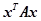 的规范形;
的规范形;
(Ⅱ)证明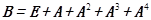 是正定矩阵,并求行列式
是正定矩阵,并求行列式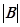 的值。
的值。
-
(本题满分11分)
设二维随机变量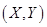 的概率密度为
的概率密度为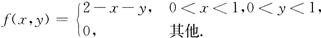
(Ⅰ)求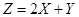 的概率密度函数
的概率密度函数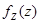 ;
;
(Ⅱ)计算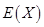 ,
,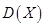 ;
;
(Ⅲ)计算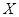 与
与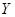 的相关系数。
的相关系数。
-
(本题满分11分)
设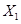 ,
,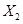 是来自总体X的简单随机样本,
是来自总体X的简单随机样本,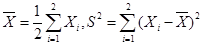 分别为样本的均值和方差,Y=
分别为样本的均值和方差,Y=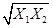 .
.
(Ⅰ)当X服从数学期望为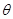 的指数分布时,EY=
的指数分布时,EY=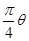 ;
;
(Ⅱ)当x~N(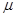 ,
,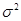 )时,
)时,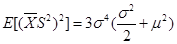 .
.
-
对于函数Y=
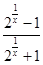 ,点x=0是( ).
,点x=0是( ).
-
设函数
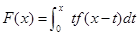 ,
,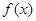 为连续函数,f(0)=0,
为连续函数,f(0)=0,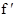 (x)﹥0,则y=F(x)在(0,+∞)内是( ).
(x)﹥0,则y=F(x)在(0,+∞)内是( ).
-
已知
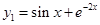 ,
,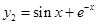 ,
,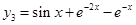 ,则以
,则以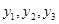 为解的二阶线性非齐次方程为( ).
为解的二阶线性非齐次方程为( ).
-
设
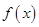 在
在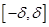 有定义,且
有定义,且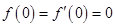 ,
,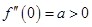 ,又
,又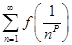 收敛,则P的取值范围是( ).
收敛,则P的取值范围是( ).
-
若P,Q均为n阶方阵,且
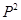 =P,
=P,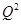 =Q.又E-(P+Q)非奇异,则( ).
=Q.又E-(P+Q)非奇异,则( ).
-
设A,B,C,D是4个四阶矩阵,其中A≠0,︱B︱≠0,︱C︱≠0,D≠0,且满足ABCD=0,若
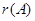 +
+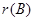 +
+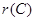 +
+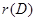 =r,则r的取值范围是( ).
=r,则r的取值范围是( ).
-
设随机变量
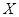 与
与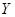 相互独立,且
相互独立,且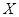 服从区间(0,2)上的均匀分布,
服从区间(0,2)上的均匀分布,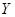 服从参数为1的指数分布,则概率
服从参数为1的指数分布,则概率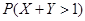 的值为( )。
的值为( )。
-
设
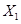 ,
,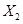 ,…,
,…,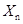 为来自总体X~N(0,
为来自总体X~N(0,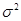 )的简单随机样本,则
)的简单随机样本,则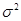 的无偏估计量为( ).
的无偏估计量为( ).
-
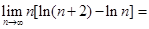 ---------.
---------.
-
曲线y=xsinx在
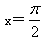 的曲率k=---------.
的曲率k=---------.
-
设
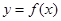 二阶可导,且
二阶可导,且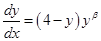 ,
,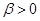 ,若
,若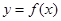 的一个拐点是(
的一个拐点是(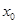 ,3),则
,3),则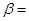 ------------.
------------.
-
函数
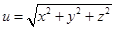 在点
在点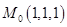 处沿曲面
处沿曲面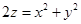 在点
在点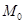 处外法线方向
处外法线方向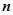 的方向导数
的方向导数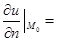 ----------.
----------.
-
设n阶矩阵A满足
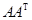 =E(E是n阶单位矩阵,
=E(E是n阶单位矩阵,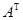 是A的转置,则︱A+E︱----------.
是A的转置,则︱A+E︱----------.
-
设4重Bernoulli试验中,已知成功的概率为P,则在没有出现全部“失败”的情况下,“成功”不止一次的概率为---------.
-
(本题满分10分)
计算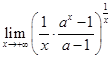 ,其中a>0且a≠1.
,其中a>0且a≠1.
-
(本题满分10分)
假定下列微分方程初值问题有唯一解,试确定u(t):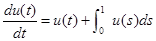 ,
,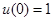 .
.
-
(本题满分10分)
设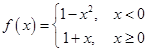 ,求
,求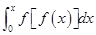 及
及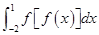 .
.
-
(本题满分10分)
设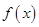 在
在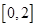 内二阶连续可导,且
内二阶连续可导,且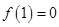 ,证明:
,证明:
(Ⅰ)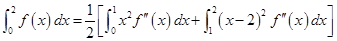 ;
;
(Ⅱ)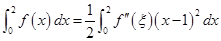 ,其中
,其中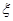 在1与
在1与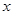 之间;
之间;
(Ⅲ)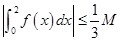 ,其中
,其中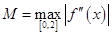 .
.
-
(本题满分10分)
设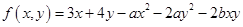 ,试问参数
,试问参数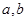 满足什么条件时,
满足什么条件时,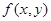 有唯一的极大值?参数
有唯一的极大值?参数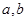 满足什么条件时,
满足什么条件时,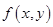 有唯一的极小值?
有唯一的极小值?
-
(本题满分11分)
设A,B为三阶相似非零实矩阵,矩阵A=(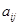 )满足
)满足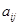 =
=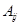 (i,j=1,2,3),
(i,j=1,2,3),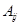 为
为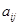 的代数余子式,矩阵B满足︱E+2B︱=︱E+38︱=0,计算行列式︱
的代数余子式,矩阵B满足︱E+2B︱=︱E+38︱=0,计算行列式︱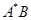 -
-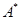 +B-E︱.
+B-E︱.
-
(本题满分11分)
已知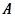 是3阶矩阵,
是3阶矩阵,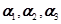 是3维线性无关列向量,且
是3维线性无关列向量,且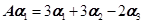 ,
,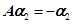 ,
,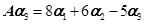 。
。
(Ⅰ)写出与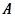 相似的矩阵B;
相似的矩阵B;
(Ⅱ)求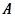 的特征值和特征向量;
的特征值和特征向量;
(Ⅲ)求秩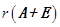 。
。
-
(本题满分11分)
设有一批产品成箱出售,每箱有产品10件,各箱含1件次品,2件次品,3件次品的概率分别为60%,20%和20%。顾客购买时,由售货员随意选一箱,顾客开箱任取4件进行检验,若发现次品不多于1件,则确定购买此箱产品,否则不买。
(Ⅰ)求顾客购买一箱产品的概率;
(Ⅱ)若顾客共挑选150箱这样的产品,求确定购买产品箱数的数学期望与方差。
-
(本题满分11分)
某商品一周的需求量X是随机变量,已知X的概率密度为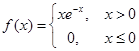 ,假设各周的需求量相互独立,以U;表示k周的总需求量,试求:
,假设各周的需求量相互独立,以U;表示k周的总需求量,试求:
(I)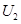 和
和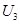 的概率密度
的概率密度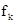 (x)(k=2,3);
(x)(k=2,3);
(II)接连三周中的周最大需求量的概率密度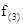 (x).
(x).
-
设
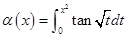 ,
,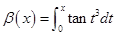 ,
,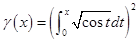 ,将
,将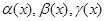 排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列顺序为( ).
排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列顺序为( ).
-
定积分
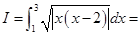 ( ).
( ).
-
设p(x)为区间[0,1]上的正值连续函数,a与b为任意常数,区域D={(x,y)︱0≤x,y≤1},则
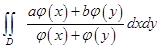 ( ).
( ).
-
已知级数
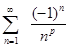 与反常积分
与反常积分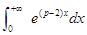 均收敛,则P的取值范围是( ).
均收敛,则P的取值范围是( ).
-
设
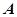 为n阶矩阵,对于齐次线性方程(Ⅰ)
为n阶矩阵,对于齐次线性方程(Ⅰ)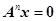 和(Ⅱ)
和(Ⅱ)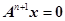 ,则必有( ).
,则必有( ).
-
已知向量
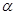 ,
,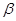 ,
,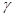 线性无关,则k≠1是
线性无关,则k≠1是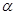 +
+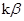 ,
,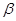 +
+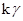 ,
,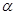 +
+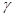 线性无关的( ).
线性无关的( ).
-
设
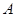 、
、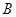 、
、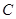 为3个随机事件,且
为3个随机事件,且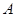 、
、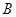 相互独立,则下列命题中不正确的是( ).
相互独立,则下列命题中不正确的是( ).
-
将一枚硬币抛n次,X表示正面向上的次数,Y表示反面向上的次数,则X和Y的相关系数为( ).
-
已知曲线
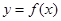 在点(1,0)处的切线在y轴上的截距为-1,则
在点(1,0)处的切线在y轴上的截距为-1,则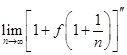
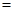 -----------.
-----------.
-
设
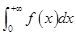 收敛,
收敛,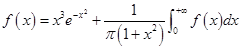 ,则
,则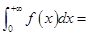 -----------。
-----------。
-
设函数z=f(x,y)的二阶偏导数存在,
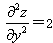 ,且f(x,0)=1,
,且f(x,0)=1,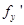 (x,0)=x,则f(x,y)=-----------.
(x,0)=x,则f(x,y)=-----------.
-
若级数
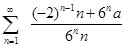 收敛,则a=-----------.
收敛,则a=-----------.
-
设三阶方阵A=(
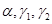 ),B=(β,
),B=(β,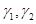 ),其中α,β,
),其中α,β,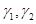 均为三维列向量,且|A|=2,|B|=4,则|2A-3B|=-----------.
均为三维列向量,且|A|=2,|B|=4,则|2A-3B|=-----------.
-
设随机变量
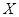 服从参数为1的Poisson分布,随机变量
服从参数为1的Poisson分布,随机变量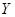 服从参数为2的Poisson分布,且
服从参数为2的Poisson分布,且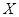 与
与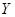 相互独立,则
相互独立,则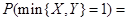 ----------.
----------.
-
(本题满分10分)
[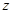 ]表示不超过
]表示不超过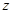 的最大整数,试确定常数
的最大整数,试确定常数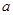 的值,使
的值,使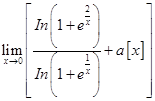 存在,并求出此极限。
存在,并求出此极限。
-
(本题满分10分)
设有摆线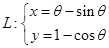 ,
,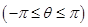 试求:
试求:
(Ⅰ)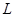 绕
绕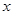 轴旋转一周所得旋转面的面积;
轴旋转一周所得旋转面的面积;
(Ⅱ)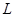 上任意点处的曲率;
上任意点处的曲率;
(Ⅲ)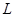 与
与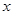 轴所围平面图形的形心
轴所围平面图形的形心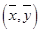 。
。
-
(本题满分10分)
设f(x)在[0,1]上连续.
(Ⅰ)证明至少存在一个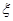 ∈(0,1),使得
∈(0,1),使得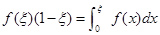 ;
;
(Ⅱ)若f(x)为可导函数且满足(1-x)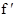 (x)﹥2f(x),证明
(x)﹥2f(x),证明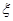 是唯一的.
是唯一的.
-
(本题满分10分)
设L是y=asinx(a>0)上从(0,0)到(π,0)的一段曲线,求a的值,使曲线积分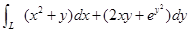 取得最值.
取得最值.
-
(本题满分10分)
设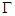 是
是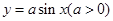 上从(0,0)到(
上从(0,0)到(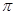 ,0)的一段曲线,求
,0)的一段曲线,求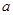 的值,使曲线积分
的值,使曲线积分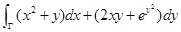 取得最大值。
取得最大值。
-
(本题满分11分)
已知矩阵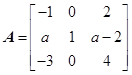 有三个线性无关的特征向量,求
有三个线性无关的特征向量,求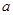 的值,并求
的值,并求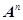 。
。
-
(本题满分11分)
设A为三阶矩阵,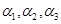 为对应特征值
为对应特征值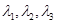 的特征向量,令β=
的特征向量,令β=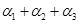 .若
.若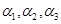 为Bx=0的基础解系,试求β,Aβ,
为Bx=0的基础解系,试求β,Aβ,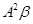 也为Bx=0的基础解系的条件.
也为Bx=0的基础解系的条件.
-
(本题满分11分)
设随机变量X的概率密度为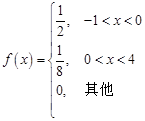 ,记随机变量
,记随机变量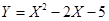 .
.
(Ⅰ)求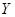 的密度函数;
的密度函数;
(Ⅱ)计算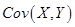 。
。
-
(本题满分11分)
设总体X服从均匀分布U(θ,2θ),其中θ未知(θ>0),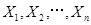 为取自总体X的简单随机样本.
为取自总体X的简单随机样本.
(Ⅰ)求θ的矩估计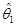 ;
;
(Ⅱ)求θ的最大似然估计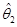 ;
;
(Ⅲ)判断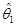 和
和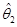 是否为θ的无偏估计量.
是否为θ的无偏估计量.
-
已知x=0是函数y=
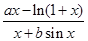 的可去间断点,则常数a,b的取值范围是( )。
的可去间断点,则常数a,b的取值范围是( )。
-
设有无穷级数
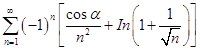 ,其中
,其中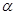 为常数,则此级数( )。
为常数,则此级数( )。
-
设
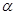 、
、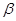 、
、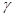 均为大于1的常数,则级数
均为大于1的常数,则级数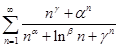 ( )。
( )。
-
已知级数
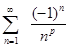 与反常积分
与反常积分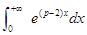 均收敛,则P的取值范围是( )。
均收敛,则P的取值范围是( )。
-
如果向量β可由向量组
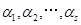 线性表示,则( )。
线性表示,则( )。
-
设
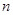 维列向量
维列向量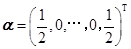 ,矩阵
,矩阵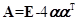 ,其中
,其中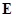 是
是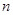 阶单位矩阵,若
阶单位矩阵,若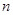 维列向量
维列向量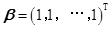 ,则向量
,则向量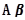 的长度为( )。
的长度为( )。
-
将一枚硬币抛n次,X表示正面向上的次数,Y表示反面向上的次数,则X和Y的相关系数为( )。
-
设随机变量X,Y独立同分布于N(0,1),则( )。
-
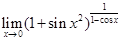 =------------.
=------------.
-
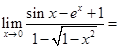 ----------.
----------.
-
设曲线
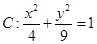 ,取逆时针方向,则
,取逆时针方向,则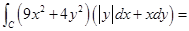 -----------.
-----------.
-
微分方程y''+4y'+4y-
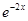 的通解为-----------.
的通解为-----------.
-
已知二次曲面
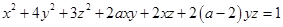 是椭球面,则
是椭球面,则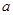 的取值为----------.
的取值为----------.
-
设随机变量X,Y相互独立且都服从区间[1,3]上的均匀分布,引进事件A={X≤a),B={Y>a),若P{AUB}=
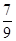 ,则a=----------.
,则a=----------.
-
(本题满分10分)
设f(x)在[0,1]上可导,且f(0)=0,又f(x)满足关系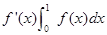 =25,求f(x).
=25,求f(x).
-
(本题满分10分)
求幂级数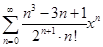 在其收敛域内的和函数。
在其收敛域内的和函数。
-
(本题满分10分)
证明: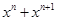 +…+x=1(n>1)在(0,1)内必有唯一实根
+…+x=1(n>1)在(0,1)内必有唯一实根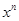 ,并求
,并求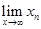 .
.
-
(本题满分10分)
已知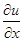 =2x+y+1,
=2x+y+1,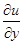 =x+2y+3,u(0,0)=1,求u(x,y)及其极值.
=x+2y+3,u(0,0)=1,求u(x,y)及其极值.
-
(本题满分10分)
如果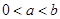 ,
,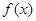 在
在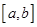 上连续,在
上连续,在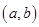 内可导,试证:在
内可导,试证:在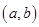 内存在
内存在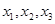 使
使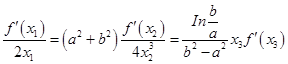 。
。
-
(本题满分11分)
已知向量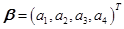 可以由
可以由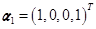 ,
,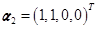 ,
,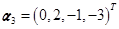 ,
,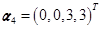 线性表出。
线性表出。
(Ⅰ)求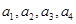 应满足的条件;
应满足的条件;
(Ⅱ)求向量组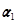 ,
,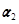 ,
,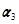 ,
,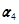 的一个极大线性无关组,并把其他向量用该极大线性无关组线性表出;
的一个极大线性无关组,并把其他向量用该极大线性无关组线性表出;
(Ⅲ)把向量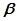 分别用
分别用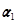 ,
,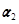 ,
,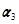 ,
,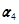 和它的极大线性无关组线性表出。
和它的极大线性无关组线性表出。
-
(本题满分11分)
已知方程组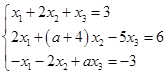 有无穷多解,矩阵
有无穷多解,矩阵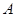 的特征值是1,-1,0,对应的特征向量依次是
的特征值是1,-1,0,对应的特征向量依次是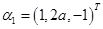 ,
,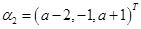 ,
,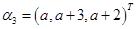 。
。
(Ⅰ)求矩阵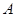 ;
;
(Ⅱ)求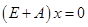 的基础解系。
的基础解系。
-
(本题满分11分)
设某地区在一年内发生一般性交通事故的次数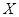 和发生重大交通事故的次数
和发生重大交通事故的次数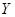 相互独立,且分别服从参数为
相互独立,且分别服从参数为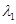 和
和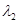 的泊松分布。试求在一年内共发生了
的泊松分布。试求在一年内共发生了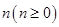 次交通事故的条件下,重大交通事故
次交通事故的条件下,重大交通事故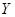 ,的条件概率分布。
,的条件概率分布。
-
(本题满分11分)
设总体X服从均匀分布U(θ,2θ),其中θ未知(θ>0),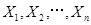 为取自总体X的简单随机样本。
为取自总体X的简单随机样本。
(Ⅰ)求θ的矩估计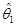 ;
;
(Ⅱ)求θ的最大似然估计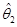 ;
;
(Ⅲ)判断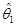 和
和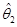 是否为θ的无偏估计量.
是否为θ的无偏估计量.
 Copyright 2023 上海欣师教育科技有限公司
Copyright 2023 上海欣师教育科技有限公司